Решение простых и составных задач

Следующий важный вопрос касается решения простых и составных задач. С математической точки зрения простой называют задачу, которая решается одним действием. Всякая числовая задача, разрешимая не одним действием. Всякая числовая задача, разрешимая не одним, а несколькими действиями, в соответствующем порядке их следования, называется составной задачей.

Наличие этого разделения вовсе не означает, что оно может быть прямо перенесено в методику обучения решению задач. Здесь должен быть выработан педагогически целесообразный путь, способствующий оптимальной эффективности методических приемов для общего и математического развития школьников.

Когда ребята освоились с зависимостью между данными задачи и искомым и могут осмысленно найти способ решения, можно перейти к задачам в два действия. И здесь надо применить сопоставление. Например, задача в одно действие: «Ира купила сначала 6 тетрадей, а затем ещё 2. Сколько всего тетрадей купила Ира?» Дети решают задачу. Затем включается задача в два действия. Учительница записывает на доске:

– Вот мы решили первую задачу и узнали, что Ира купила всего 8 тетрадей. Как же мы будем решать вторую задачу? Что в ней спрашивается? [Сколько тетрадей осталось у Иры?]

– А почему спрашивается, сколько тетрадей осталось у Иры? [Потому что она 3 тетради дала брату]. Можно ли узнать сколько тетрадей осталось у Иры, если мы не знаем, если мы не знаем сколько всего тетрадей она купила? [Нет, нельзя.] А как узнать, сколько всего тетрадей она купила? [Надо сложить 6 тетрадей и 2 тетради, потому что Ира купила сначала 6 тетрадей, а потом – еще 2 тетради]. Складываем. Сколько получилось? [8 тетрадей.] Значит, Ира купила всего 8 тетрадей. Из этих 8 тетрадей 3 тетради Ира дала брату. Как же узнать, сколько тетрадей осталось у Иры, если она купила всего 8 тетрадей, а брату дала 3 тетради? [Надо из 8 тетради вычесть 3 тетради. Получится 5 тетрадей. Значит, у Иры осталось 5 тетрадей.] Учительница записывает ход решения на доске в правом столбце.

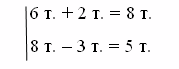
Тогда на доске появляется такая запись решения первой и второй задачи:

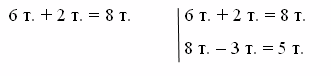
Чем же отличается друг от друга первая и вторая задачи? Первая решается одним действием, вторая – двумя действиями. Когда решаем первую, мы сразу сможем ответить на вопрос задачи. Когда решаем первую, мы сразу можем ответить на вопрос задачи. Когда решаем вторую задачу, сразу на вопрос задачи ответить не можем. Поэтому первая задача решается одним действием, вторая – двумя. [1]

Л.В. Занков считает полезным, кроме того, сопоставление таких задач, которые отличаются главным образом тем, какая жизненная ситуация отражена в каждой из них. Если при этом в задачах фигурируют одни и те же лица, одни и те же действия, одни и те же объекты, тогда зависимость хода решения задачи от своеобразия приведенной в ней жизненной ситуации выступает наиболее выпукло. Вот три задачи, которые могут служить материалом для сопоставления.

Задача 1. Мальчик выстругал несколько палочек. Три палочки он отдал сестре, и тогда у него осталось 15. Сколько палочек выстругал мальчик?

Задача 2. Мальчик выстругал 7 палочек, а всего ему нужно выстругать 12 палочек. Сколько палочек ему осталось выстругать?

Подробно о педагогике:

Взаимодействие субъектов образовательного процесса в диагностико-коррекционной работе
Содержание учебного материала Психолого-медико-педагогическая консультация (комиссия), её роль в предупреждении и коррекции отклонений в развитии и поведении ребёнка. Школьный консилиум – рабочий орган взаимодействия педагогов и специалистов, участвующих в диагностико-коррекционной работе с детьми ...

Интенсивное обучение – определение понятия
За последние годы достигнуты многообещающие результаты в практике интенсивного обучения иностранным языкам самого различного контингента учащихся. Интенсивные методы осмысливаются как оптимальная реализация некоторых прогрессивных тенденций в общей педагогике и психологии, в частности, в контексте ...

Применение дидактического материала при обучении построению простых предложений и их распространении
С начала обучения коррекционная работа проводилась по накоплению словарного запаса, обучению практическому употреблению категорий единственного и множественного числа существительных и глаголов настоящего и прошедшего времени, образованию категорий притяжательных местоимений, параллельно с этой раб ...