Ключевые психологические идеи тренинга

Новизна курса заключается в применении указанных выше методов и приемов для решения конкретных математических задач, и их использование при разрешении жизненных проблемных ситуаций.

Каждое из занятий состоит из трех взаимосвязанных этапов:

на первом этапе деятельность учителя была направлена на формирование у школьников понимания идеи нового приема;

второй этап направлен на осознание учащимися применения выделенного приема в бытовых ситуациях;

на третьем этапе школьники учились использовать прием при решении конкретных математических задач.

Кроме того, в начале каждого занятия ученикам предлагается проблемная ситуация, попытки разрешения которой зачастую приводят к неэффективному решению, в основном из-за использования только раннее изученных методов или жизненного опыта. В такой работе происходит актуализация знаний, после чего ученики «подталкиваются» педагогом к наиболее оптимальному и эффективному решению, обобщение которого приводит к новому приему активизации мышления.

Данный курс образует комплексную методику развития креативности на основе кружковых занятий по математике в средней школе, благодаря включению в образовательный процесс инструментов ТРИЗ-педагогики.

Таким образом, разработанный курс призван подтвердить гипотетические положения выпускной квалификационной работы.

Опытно-экспериментальная работа осуществлялась в МОУ СОШ с УИОП № 21 г. Кирова и МОУ СОШ № 57 г. Кирова.

В МОУ СОШ с УИОП № 21 г. Кирова был проведен полностью курс «Тренинг креативного мышления» (9 занятий):

в 7-б и 8-б классах с углубленным изучением математики (июнь 2007 г.);

в общеобразовательном 8-в классе (декабрь 2007 г.).

В МОУ СОШ № 57 г. Кирова был проведен краткий курс «Тренинг креативного мышления» (2 занятия) в 10-б классе с профильным уровнем изучения математики (февраль 2008 г.).

Для проверки гипотетических положений был использован комплексный метод, который включает в себя теоретический анализ психологической, педагогической литературы по изучаемой проблеме, включая наблюдение, беседы, формирующий эксперимент, тестирование с применением теста креативности Е. П. Торренса (для 8-в класса), теста Дж. Гилфорда (для 7-б и 8-б классов), статистические методы обработки материалов (статистику Хотеллинга, критерий Уилкоксона).

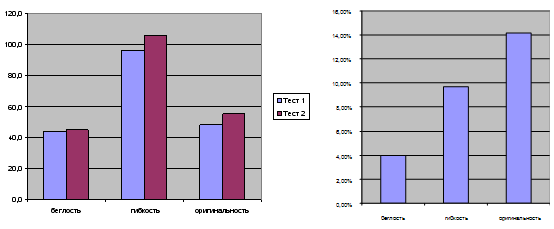
1. Сравним средние результаты изучаемых параметров (беглость, гибкость, оригинальность) в начале и конце эксперимента отдельно. Для этого наглядно представим результаты опытно-экспериментальной работы (диаграмма 1), рассмотрев в прямом сравнении (слева), и относительный рост уровня креативности по исследуемым параметрам (справа).

В экспериментальной группе по всем трем параметрам наблюдается рост показателей от 4% до 14%.

2. Используя многомерные методы статистического анализа (статистику Хотеллинга), заключаем, что есть основания на указание существенного различия общей креативности школьников экспериментальной группы до и после эксперимента (см. Приложение 2).

Диаграмма 1

Результаты оценки исследуемых параметров в начале (тест 1) и конце эксперимента (тест 2) у экспериментальной группы

3. Определим характер изменения показателей экспериментальной группы, применив критерий Уилкоксона. Сформулируем нулевую гипотезу : «предлагаемая методика не способствует улучшению параметров креативности (соответственно беглости, гибкости и оригинальности)». Тогда конкурирующая гипотеза будет определяться следующим образом: «предлагаемая методика способствует улучшению параметров креативности (соответственно беглости, гибкости и оригинальности)».

По данным таблицы для параметра «беглость» получаем меньшее сумма рангов относиться к положительным разностям. При уровне значимости критическое значение статистики . Таким образом, и нулевая гипотеза отклоняется и принимается конкурирующая гипотеза : «предлагаемая методика приобщения школьников к опыту творческой деятельности способствует улучшению беглости мышления».

Подробно о педагогике:

Опытно-экспериментальной работы по развитию познавательного интереса у младших школьников через дидактическую игру
Констатирующий эксперимент проводился в 2008/2009 учебном году на базе МОУ СОШ №18 г. Череповца, в нем участвовали ученики 1 «А» класса, в количестве 26 человек, обучающиеся по учебнику «Русская азбука» под редакцией В.Г. Горецкого. Следует отметить, что к концу 1 класса учащиеся должны знать: все ...

Анализ опыта работы БОУ "СОШ №162"
Исследование проводилось в марте 2013 года с использованием следующих методов: беседа, анкетирование классного руководителя, диагностика уровня развития коммуникативных универсальных учебных действий 4 класса (22 человека) по диагностике "Что любит мишка?". Цель анкетирования: установить ...

Специфика развития математических способностей
Ребенок должен использовать умения сравнивать, классифицировать, анализировать и обобщать результаты своей деятельности. Логические приемы умственных действий - сравнение, обобщение, анализ, синтез, классификация, сериация, аналогия, систематизация, абстрагирование - в литературе также называют лог ...