Использование инструментов ТРИЗ

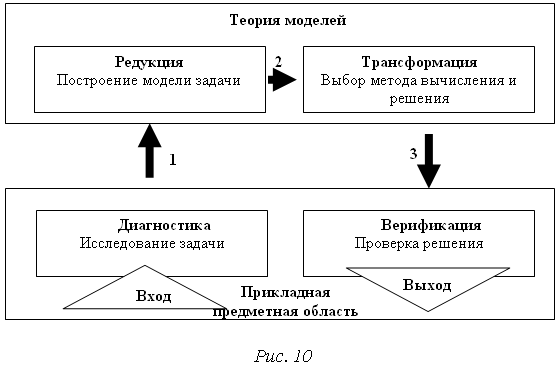
Рассмотрим обобщенную схему мета-алгоритма изобретения (рис. 9, Prof. Dr. Dr. Sc. techn. M. Orloff, Modern TRIZ Academy International, Berlin), а также упрощенный мета-алгоритм для решения некоторого класса учебных математических задач (рис. 10).

Тогда ход решения задачи можно уложить в 4 крупных этапа:

диагностика (исследование задачи),

редукция (построение модели задачи (алгебраической, аналитической и др.)),

трансформация (выбор метода решения (вычисления) модели),

верификация (проверка решения).

При этом данная схема совпадает с методикой организации решения учебной математической задачи соблюдением формально-логической схемы рассуждения «анализ – построение – доказательство – исследование» при решении геометрических задач на построение и т.п. [39, 82].

Переходы 1 и 3 требуют знания теории моделей и прикладных областей ее применения. Переход 2 требует умения строить и решать модели теории.

Пример 5. В двух цехах завода стоят станки двух типов. Первого типа 2 и 1 соответственно в первом и втором цехе, второго – 6 и 2. Определите среднею мощность, потребляемой станком каждого типа, если первый цех потребляет 340 киловатт-часов, второй – 130.

Решение представим в виде мета-алгоритма (рис. 11).

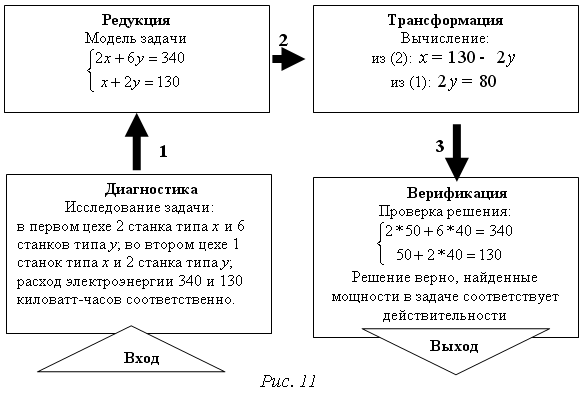
Пусть в двух цехах завода работает разное количество станков двух типов. Для точного определения средней мощности, потребляемой станком определенного типа, было решено воспользоваться имеющимися измерениями расхода электроэнергии по каждому цеху за сутки. На этапе диагностики проблемы было установлено количество станков каждого типа и данные по потреблению электроэнергии. На этапе редукции была построена система из двух линейных уравнений с двумя неизвестными. На этапе трансформации из двух простейших подходящих методов (метод исключения переменных и метод замены и подстановки переменных) выбрали последний. На этапе верификации путем прямой подстановки полученных значений искомых переменных в исходные уравнения убедились в правильности решения задачи.

Этот пример служит практической иллюстрацией абстрактной схемы, приведенной на рис. 10.

Пример 6. Что больше или ?

Решение представлено на рис. 12. Необходимо сравнить два числа. На этапе диагностики проблемы было установлено что непосредственное сравнение затруднительно. На этапе редукции была построена функция (обобщение по двум ее значениям) . На этапе трансформации из методов доказательства монотонности функции выбрали наиболее подходящий с использованием производной . На этапе верификации доказали монотонность.

На этапе верификации путем исследования полученного решения убедились в правильности решения задачи.

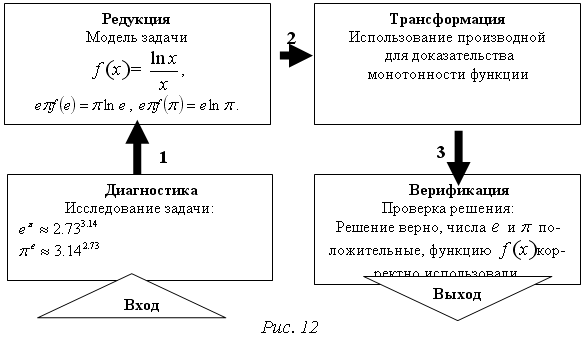
Таким образом, при использовании мета-алгоритма для решения учебных математических задач появляется возможность наглядней представлять ход решения задачи.

Причем на этапах диагностики и редукции преимущественно используется анализ (проблемы решения), на этапах трансформации и верификации – синтез (идеи решения). Тем самым, используя при решении задачи мета-алгоритм, ребенок на уроках математики осознано учиться использовать разные способы мышления.

Обучение – это замена удивления пониманием …

Подробно о педагогике:

Практическое формирование интереса к обучению
Формирование интереса к учению является важным средством повышения качества обучения школьников. Отношение учащихся к тому или иному предмету определяется различными факторами: индивидуальными особенностями личности, особенностями самого предмета, методикой его преподавания. Увлекательный материал, ...

Методика работы по развитию звуковой культуры речи
Овладение произношением всех звуков родного языка к пяти годам возможно при правильном руководстве развитием речи детей. Целенаправленное обучение, использование соответствующей методики создают условия для реализации имеющихся у детей предпосылок. Формирование звуковой стороны речи осуществляется ...

Предрасполагающие и вызывающие факторы возникновения заикания у детей дошкольного возраста
До сих пор нет единой научно обоснованной теории, с позиций которой можно было бы обобщить и систематизировать экспериментальные данные и различные гипотезы, высказанные многими авторами по поводу причин возникновения этого нарушения речи. В то же время все исследователи сходятся во мнении, что при ...