Использование инструментов ТРИЗ

Пример 11. Отрицательные числа получаются из положительных применением принципа инверсии.

Пример 12. Иррациональные числа получаются из рациональных применением принципа непрерывности полезного действия: числа занимают непрерывно всю числовую ось.

Пример 13. Комплексные числа получаются из вещественных применением принципа перехода в другое измерение: от числовой прямой к числовой комплексной плоскости.

Пример 14. Переменные получаются из постоянных применением принципа динамичности.

Пример 15. Функции одной переменной получаются из одиночных переменных по закону перехода в бисистему.

Пример 16. Функции нескольких переменных получаются из одиночных переменных по закону перехода в полисистему.

Пример 17. Создание Ньютоном и Лейбницем интегрального исчисления – классический пример перехода на микроуровень.

Таким образом, можно аналогично рассуждать в отношении других математических объектов, используя метод переизобретения знаний. Использовать данный метод можно на факультативных занятиях. Учащаемся наглядно показывается, как их уровень знакомства с математикой соответствует общим законам развития систем.

В конце первой главы в инструменты ТРИЗ-педагогики мы включили методы мышления, не относящиеся собственно к ТРИЗ. По сравнению классическими инструментами ТРИЗ методы технического творчества лучше отработаны при использовании их в учебном процессе [22, 42, 67, 68, 70] начиная с начальной школы [20, 28, 29, 87], но об использовании данных методов при обучении школьников математике литературы не встречается, хотя они являются ценным дидактическим материалом.

К основным методам научного творчества можно отнести: метод проб и ошибок; метод морфологического анализа; мозговой штурм; синергетику.

Данные методы достаточно легко можно применять при решении учебных математических задач.

Пример 18. В каком случае произведение двух натуральных чисел дает четное число?

Используем метод проб и ошибок, переберем все возможные варианты четности двух чисел. И сделаем соответствующий вывод. В альтернативу можно показать применение идеального конечно результата ТРИЗ, сформулировав, что произведение данных чисел дало четной число , тогда вывод о необходимости четности хотя бы одного из них достаточно логичен.

При решении многих математических задач при использовании метода проб и ошибок другого математического аппарата рассуждений, учащиеся осознанно усваивают ценность математики.

Пример 19. Укажите способы определения высоты здания без сложных приборов.

Коллективное (групповое) решение этой задачи методом мозгового штурма приводит к разнообразным выводам. Наиболее оптимальное и эффективное из них, как правило, попутно подводит к изучению темы «Подобные треугольники» [76].

Рассмотрим два из возможных вариантов решения. Первый вариант предполагает, что человек AB стоит и смотрит на здание ED (рис. 16). Измерив расстояния AD и AO, зная свою высоту AB, можно рассмотреть подобные треугольники BEC и ОВА, из соотношения сторон которых можно

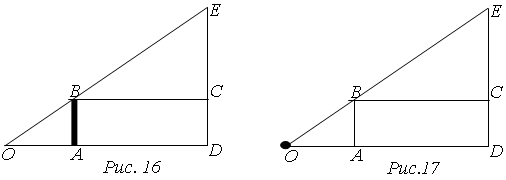
узнать искомое.

Второй вариант решения предполагает, что человек смотрит из точки О на некоторый предмет AB, высоту которого мы можем измерить, например, палку (рис. 17). Тогда из подобия тех же треугольников, что и в первом варианте с легкостью находится искомое.

Другие контрольные ответы заключается с применением тени, зеркала и построение высотомеров [59].

Подробно о педагогике:

Модель учебного предмета
Большую роль играет моде­лирование в предметной, графической или знаковой форме способа решения задачи. Учебной моделью можно назвать такое изображение, которое фиксирует всеобщее отношение некоторого целостного объекта и обеспечивает его дальней­ший анализ. Поскольку в учебной модели изображается ...

Психолого-педагогическая характеристика учащихся 7 "АШ" и 8 "АШ" классов
На основе наблюдений и беседы с учителем была составлена краткая психолого-педагогическая характеристика учащихся 7 "АШ" и 8 "АШ" классов. Количество учащихся 7 "АШ" класса составляет 10 человек. Из них 4 мальчика и 6 девочек. Количество учащихся 8 "АШ" класс ...

Сравнительный анализ результатов исследования на этапах констатирующего и формирующего экспериментов
Целью третьего этапа является: 1) проведение повторной диагностики успеваемости при различных уровнях тревожности детей посетивших коррекционно-развивающие занятия; 2) анализ полученных в процессе первичной и повторной диагностик результатов. После осуществления формирующего эксперимента: проведени ...